- 定比例の法則の応用問題
未反応の問題
- 増加した質量(=反応した酸素の質量)に注目して,定比例の法則で計算
混合物の問題
- 求めたい質量を「x」とおく.
- xを使って,酸化銅と酸化マグネシウムの質量を定比例の法則で表す
- 加熱後の質量を用いて方程式を解く
ちょっと何を言っているかわからないですよね.
大丈夫です.わかりやすく解説していきます.
今回の問題を解く前に,こちらの計算問題を復習しておいてください.
定比例の法則とは
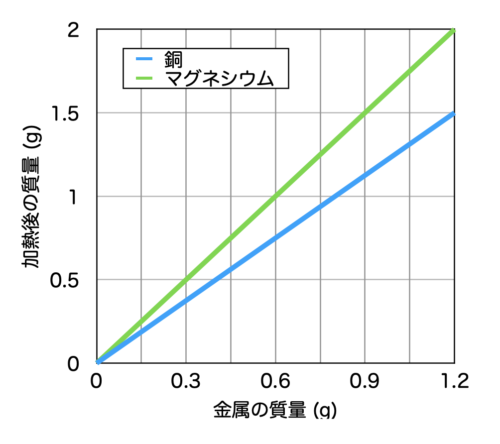
定比例の法則とは,物質が化学反応するとき,反応する物質の質量の割合は一定である法則です.
例えば,上の青色のグラフは,銅の加熱前と加熱後の質量を表しています.
銅の質量が1.2gのとき,加熱後には1.5gになっています.
つまり,銅:酸化銅 = 1.2:1.5 = 4:5となります.
したがって,銅の酸化の場合,銅:酸素:酸化銅の質量比は常に4:1:5の質量比で反応します.
また同様に,マグネシウムの燃焼の場合,マグネシウム:酸素:酸化マグネシウムは常に3:2:5の質量比で反応します.
よく出てくる反応比は覚えておくと時間の節約ができます.
覚えておくべき反応比
- Cu:O:CuO = 4:1:5
- Mg:O:MgO = 3:2:5
未反応の問題

【問題】
銅粉0.6gを加熱して反応させた.その後,質量を測定すると0.7gであった.このとき,酸素と反応せずに残った銅粉は何gか.
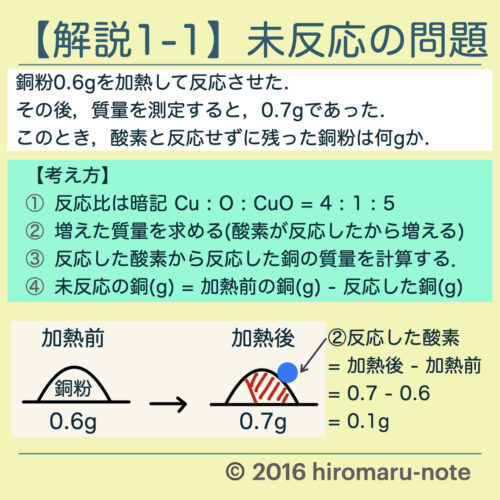
【考え方】
- 反応比は暗記する.
- Cu : O : CuO = 4 : 1 : 5
- 加熱前後での増えた質量を求める.
- 増えた質量 = 酸素が反応した質量
- 反応した酸素から反応した銅の質量を計算する.
- 未反応の銅(g) = 加熱前の銅(g) − 反応した銅(g)

【解答】
- Cu : O = 4 : 1
- 増えた質量 = 加熱後 − 加熱前
- 増えた質量 = 0.7 − 0.6 = 0.1g
- 酸素が0.1g反応したことがわかる.
- 銅と酸素の反応比で計算
- Cu : O = 4 : 1
- X : 0.1 = 4 : 1
- X = 0.4
- 酸素0.1gが銅0.4gと反応した.
- 未反応の銅 = 加熱前の銅 − 反応した銅
- 未反応の銅(g) = 0.6 − 0.4 = 0.2g
混合物の問題
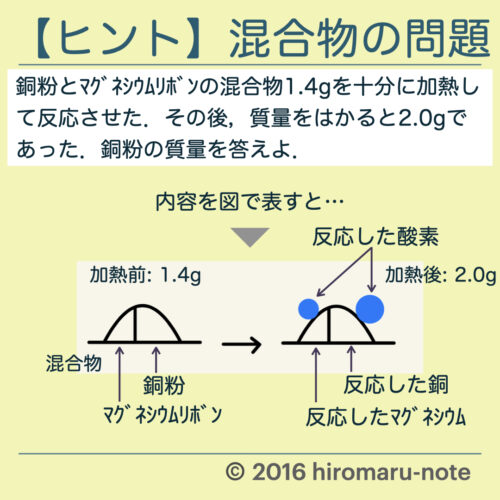
【問題】
銅粉とマグネシウムリボンの混合物1.4gを十分に加熱して反応させた.その後,質量をはかると2.0gであった.銅粉の質量を答えよ.

【考え方】
- 反応比は暗記する.
- Mg : O : MgO = 3 : 2 : 5
- 求めたい物質の質量を「x」とおいて,酸化銅と酸化マグネシウムを「x」を使って表す.
- 加熱後の質量で方程式を立てる.

【ヒント】酸化銅と酸化マグネシウムを「x」を使って表す.
- 酸化銅を「x」を使って表す.
- Cu : CuO = 4 : 5より
- x : CuO = 4 : 5
- 4CuO = 5x
- CuO = (5/4)x
- 酸化マグネシウムを「x」を使って表す.
- 問題文から加熱前の銅とマグネシウムの合計は1.4gです.
- 銅の質量をxgとしているので,マグネシウムの質量は(1.4-x)gです.
- Mg : MgO = 3 : 5より
- (1.4 – x) : MgO = 3 : 5
- 3MgO = 5(1.4 – x)
- MgO = (5/3)(1.4-x)
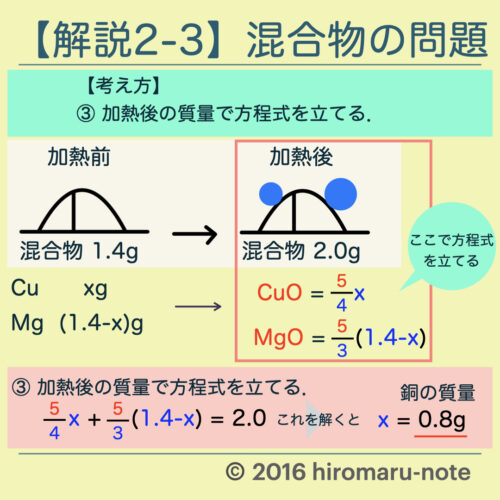
【解答】
- 反応比
- Cu : CuO = 4 : 5
- Mg : MgO = 3 : 5
- 求めたい銅の質量を「x」とおいて,CuOとMgOを質量を「x」で表す.
- CuO = (5/4)x
- MgO = (5/3)(1.4 – x)
- 加熱後の質量が2.0gなので,
- CuO + MgO = 2.0
- (5/4)x + (5/3)(1.4 – x) = 2
- 両辺12倍すると,15x + 20(1.4 – x) = 24
- 15x + 28 – 20x = 24
- 5x = 4
- x = 0.8g
まとめ:未反応や混合物の問題は偏差値60以上の人でOK
未反応の問題や混合物の問題は,偏差値60以上を目指している人が解ければOKです.
理科の苦手な人や偏差値が60以下の人は,まず基礎的な問題は解けるようにしましょう.
基礎的な問題はこちらになります.



