- 本記事の内容
地震の計算問題 – 4パターン
- P波とS波の速さを計算する(グラフ)
- 地震発生時刻を求める(文章題)
- 初期微動継続時間を求める(計算)
- 初期微動継続時間を求める(グラフ)
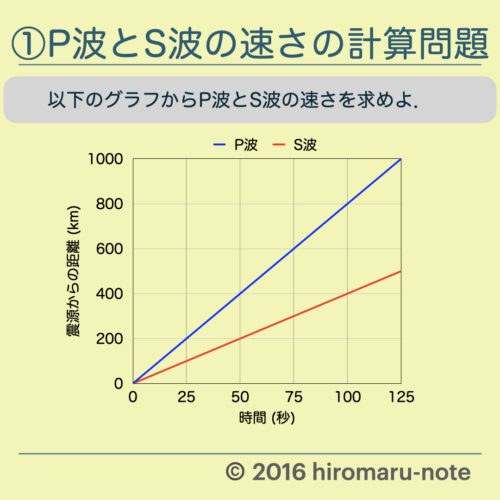
グラフからP波とS波の速さを求める
まず,グラフからP波とS波の速さを求めてみましょう.
地震の計算問題で最もよく出てくるパターンです.
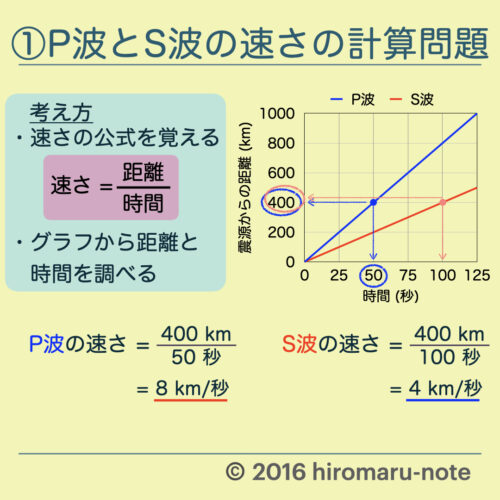
【考え方】
- 公式を覚える.
- 速さ = 距離 ÷ 時間
- グラフから距離と時間を見つける.
上の画像にあるグラフで考えてみましょう.
【解答】
P波の速さの求め方
- グラフから,50秒で400km進むことがわかります.
- それを公式【速さ = 距離 ÷ 時間】にあてはめます.
- P波の速さ = 400km ÷ 50秒 = 8km/秒
S波の速さの求め方
- グラフから,100秒で400km進むことがわかります.
- それを公式【速さ = 距離 ÷ 時間】にあてはめます.
- S波の速さ = 400km ÷ 100秒 = 4km/秒
地震発生時刻を求める
では,上の問題から地震の発生時刻を求めてみましょう.
【問題】
A地点でP波のゆれを19時34分50秒に観測した.このとき,地震発生時刻は何時か.なお,震源からA地点までの距離を400km,P波の速さを8km/秒とする.
たくさんの数字がありますが,ひとつずつ整理して考えていきましょう.
【考え方】
- 400km(震源からA地点までの距離)をP波が何秒かかるか求める.
- 地震発生時刻 = P波観測時刻 – かかった時間
【解答】
- 400km(震源からA地点までの距離)をP波が何秒かかるか求める.
- 時間 = 距離 ÷ 速さ
- 時間 = 400km ÷ 8km/秒
- 時間 = 50秒
- 地震発生時刻 = P波観測時刻 – かかった時間
- 地震発生時刻 = 19時34分50秒 – 50秒
- 地震発生時刻 = 19時34分00秒
初期微動継続時間を求める(計算)
上の問題から,初期微動継続時間を求めてみましょう.
【問題】
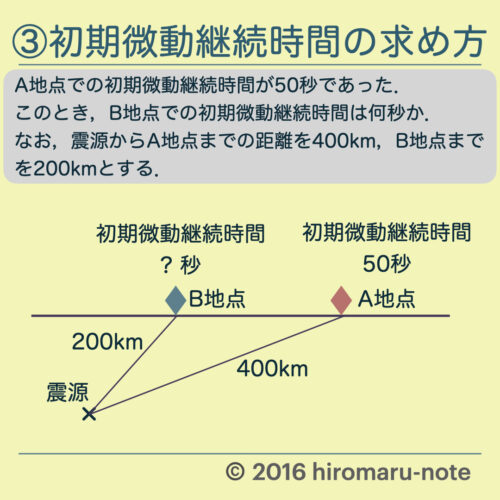
A地点での初期微動継続時間が50秒であった.このとき,B地点での初期微動継続時間は何秒か.なお,震源からA地点までの距離を400km,B地点までを200kmとする.
ここでのポイントは,震源からの距離と初期微動継続時間は比例の関係である,ということです.
【考え方】
- 覚えること → 震源からの距離と初期微動継続時間は比例
- 求めたいものを「x」とおいて,比の計算をする.
【解答】
- A地点: 400km・50秒,B地点: 200km・?秒
- 求めたいものを「x」とおいて比の計算をする.
- 400km : 50秒 = 200km : x秒
- 400x = 200 × 50
- 400x = 10000
- 4x = 100
- x = 25
- B地点の初期微動継続時間: 25秒
初期微動継続時間を求める(グラフ)
初期微動継続時間は,計算だけでなく,グラフで求められる場合もあります.
今回は,初期微動継続時間をグラフから求めることを考えます.
【問題】
B地点での初期微動継続時間は何秒か.なお,震源からB地点までの距離を200kmとする.
まず,覚えておくべきとこは,初期微動継続時間は「P波とS波のグラフの間」になります.
【考え方】
- グラフでの初期微動継続時間は,P波とS波のグラフの間
- 問題文から震源までの距離を探す
- グラフから,P波とS波のグラフの間を引き算する
今回,震源からB地点までの距離が200kmということなので,グラフの200kmのところをみます.
200km地点でのP波は25秒,S波は50秒とわかります.
【解答】
- P波とS波のグラフの間が,初期微動継続時間
- 問題文から,B地点は200kmとわかる
- グラフの200km地点では
- P波: 25秒,S波: 50秒
- 初期微動継続時間 = 50 – 25 = 25秒