以前、電気回路の問題を解く3つのコツという記事を書きました。
【電気回路が苦手な人向け】オームの法則を使って電気回路の問題を解く3つのコツ
そこでは、みんなの疑問を解決するために、3つのコツを紹介しました。
・オームの法則っていつ使うの?
・オームの法則で計算しても、答えがあわない!
今回の記事では、3つのコツの内の1つである電流の性質についてもう少し詳しく解説します。
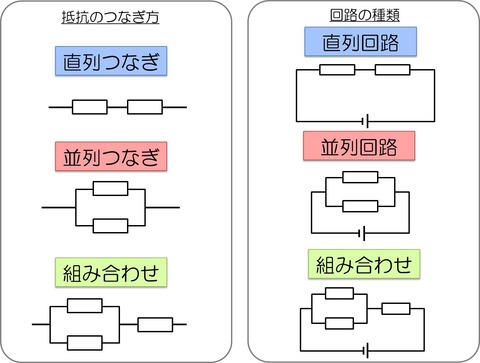
①よく出る回路のつなぎ方3パターン
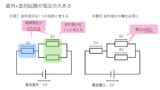
これまでに紹介したことを繰り返しになりますが、よく出る電気回路はほとんど下図の3パターンになります。
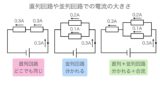
抵抗のつなぎ方には①直列つなぎ、②並列つなぎ、③直列と並列つなぎの組み合わせの3種類あります。
これら3種類がよく出る回路のパターンになります。
ここで、それぞれの回路のイメージをもっておいてください。
直列回路は、1本道
並列回路は、分かれ道
・直列回路は、1本道
・並列回路は、分かれ道
少なくとも、この3パターンの回路について①電流の大きさ、②電圧の大きさ、③オームの法則の使い方について理解すれば、必ず得点源にできます。
②電流のイメージ
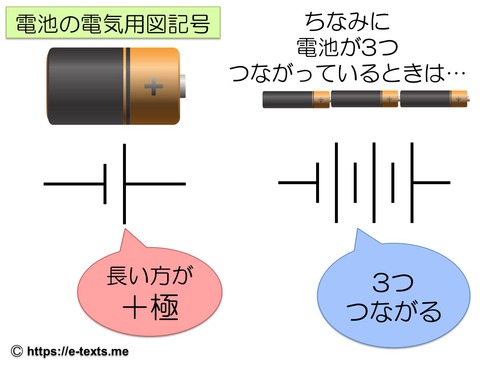
電流のイメージを持つ前に、電流はどこから流れるのか?について整理していきましょう。
電池や電源装置から電流が流れます。
そして、電気用図記号では、長い方がプラス極(+極)ということも覚えておいてください。
では、電流のイメージをもっておきましょう!
以前の記事でも紹介したのですが、
電流は、 川に流れる水 のイメージをもってください。
上の写真が電流のイメージになります。
1本の川があり、そこに水が流れています。
1本の川には、どの地点でも水の量は同じなので、
直列回路に流れる電流の大きさはどこでも同じ。
というイメージが湧くと思います。
③回路の3パターンと電流の性質
次に、3パターンの回路での電流の性質をみていきましょう。
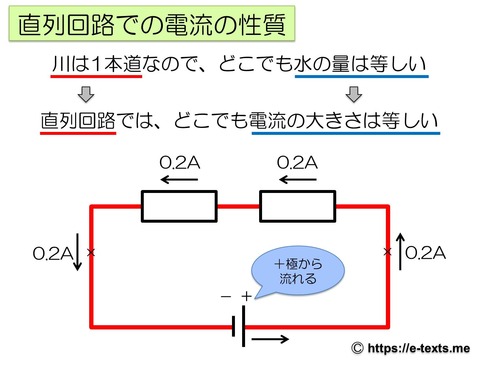
直列回路での電流の性質
まずは、直列回路での電流の性質です。
直列回路を川に見立てると、直列回路は1本道なので、どこでも水の量は等しくなります。
つまり、直列回路では、どこでも電流の大きさは等しくなります。
例えば、下の図にあるように、電池のプラス極(長い方)から0.2Aの電流が流れているとすると、2種類の抵抗に流れる電流の大きさも0.2Aずつになります。
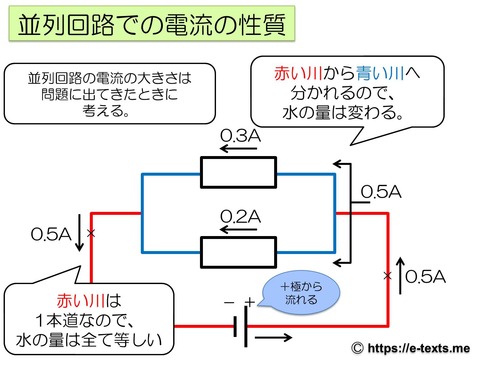
並列回路での電流の性質
並列回路は、分かれ道がありましたね。
下の図で、電池のプラス極(長い方)から0.5Aの電流が流れます。
最初は、1本道の赤い川に0.5Aの電流が流れます。
しかし、抵抗は並列につながれているので、分かれ道があり、赤い川から青い川へ分かれていきます。
今回の場合、上の抵抗に0.3A、下の抵抗に0.2Aの電流が流れました。
2つの抵抗に電流が流れた後、再び赤い川になると、上の抵抗に流れている0.3Aと下の抵抗にながれている0.2Aの電流が合流するので、再度電流の大きさは0.5Aとなります。
直列と並列回路の組み合わせでの電流の性質
最後に直列と並列回路の組み合わせでの電流の性質についてみていきましょう。
電池のプラス極(長い方)から0.5Aの電流が流れたとします。
下図の赤い川は1本道なので、0.5Aの電流が流れます。
つまり、最初の抵抗には0.5Aの電流が流れることになります。
次に、赤い川から青い川に分かれます。
今回、上の青い川に0.3A、下の青い川に0.2Aの電流が流れたとします。
すると、上の抵抗には0.3Aが、下の抵抗には0.2Aの電流が流れることになります。
並列つなぎの抵抗に電流が流れた後、再び2本の青い川は1本の赤い川になるので、0.3Aと0.2Aの電流が合流し、赤い川には0.5Aの電流が流れることになります。
理解できましたか?
一回で理解できなくても、解説文と図を何度も見て、完全に理解できるまで繰り返してください。
④電流の大きさを求めよう!
では、この記事で学習したことをつかって、電流の大きさを求めてみましょう!
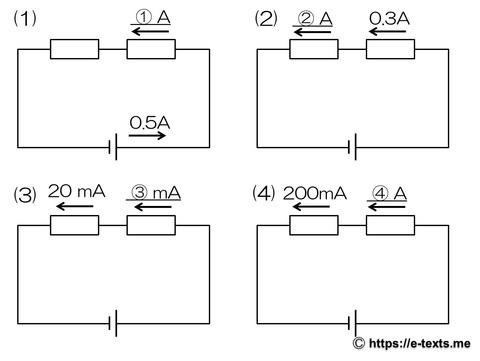
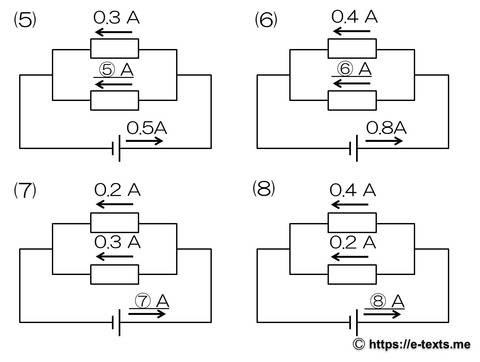
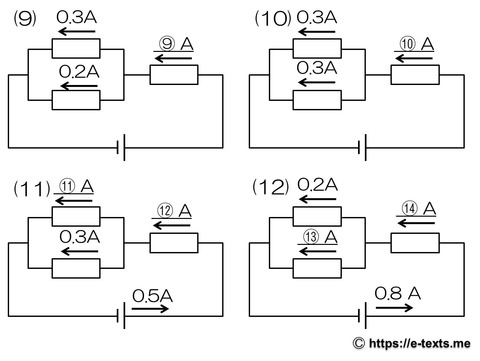
問題
解答
(1) ① 0.5 A
(2) ② 0.3 A
(3) ③ 20 mA
(4) ④ 0.2 A
(5) ⑤ 0.2 A
(6) ⑥ 0.4 A
(7) ⑦ 0.5 A
(8) ⑧ 0.6 A
(9) ⑨ 0.5 A
(10) ⑩ 0.5 A
(11) ⑪ 0.2 A ⑫ 0.5 A
(12) ⑬ 0.6 A ⑭ 0.8 A